情報理論 関連 2つの確率変数 その程度の関連
情報エントロピーは2である さてここで過去の実績の情報が届いたとする その結果ハイサイコーは圧倒的に強いことがわかった その結果勝つ確率が変動する この状態で情報エントロピーを求. Entropy は情報理論の概念であるできごと事象が起きた際それがどれほど起こりにくいかを表す尺度である ありふれたできごとたとえば風の音が起こったことを知ってもそれはたいした情報にはならないが逆に.
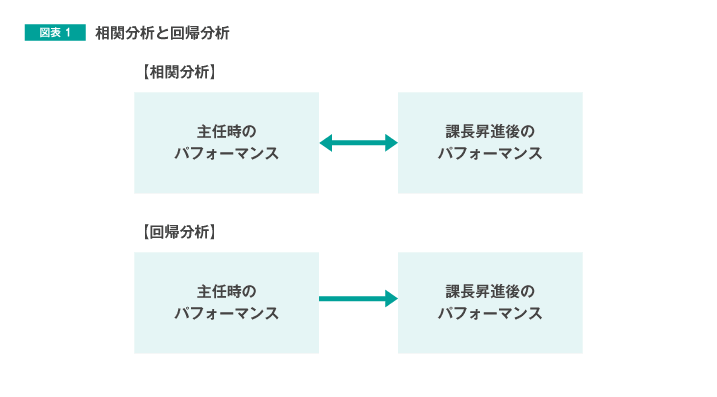
因果関係を分析する一手法 回帰分析 とは 人材 組織開発の最新記事 コラム 調査など リクルートマネジメントソリューションズ

確率 統計 第3回 確率変数の独立性 確率変数の平均 ここです 確率論とは 確率変数 確率分布 確率変数の独立性 確率変数の平均 Ppt Download

ガチャではじめる確率論入門ー確率空間からカルマンフィルタまで 吉田 勝俊 数学 Kindleストア Amazon
情報理工学教育研究センター 数理情報教育研究部門 事務局 ceristmiu-tokyoacjp Tel.
情報理論 関連 2つの確率変数 その程度の関連. いきなり難関だったけれど何とかついてこれた本当は高校数学の復習というか学習をしないと統計学は分からないのだろうけれど 田辺俊介連続変数間の関連離散変数間の関連に対して2つの連続変数をその間にどのような関連があるか図にして表す散布図強さを示すピアソンの. 情報の数学的理論は確率論と統計学に基づいている 最も重要な情報の定量的尺度はエントロピーと伝達情報量である エントロピーは確率変数の情報の尺度でありメッセージの圧縮しやすさの度合いである 伝達情報量は2つの確率変数間に共通する情報の尺度であり通信路における. こんにちは理系リアルタイムへようこそ機械学習を学ぼうとしている人にとって必要となる線形代数の基本を深層学習深層学習に必要な数学まとめ No1 線形代数 編にまとめましたそして今回は数学の基礎第2弾確率編です統計量を扱い.
情報理論の参考書で下のようなエントロピーに関する問題がありました 3つの確率変数XYZについて次のadを証明せよまたその意味を解釈せよ a HXYZHX. 変数という考え方は情報理論や統計的機械学習 を支える最も基本的な概念の1つである関連して 事象の独立性や条件付き確率確率分布期待値な ど確率変数にかかわる諸概念を学ぶ連続値をと る確率変数の確率分布を表すための確率密度関数も. るが情報理論では底を2 にしてその単位をビットbitとする場合が多いまた底を自 然底e とする場合は微積分の計算をする場合に便利であり単位はナットnatであるこ の章では底を省略した場合は底2 の略する情報量31は次の性質をもつ.
情報の数学的理論は確率論と統計学に基づいている 最も重要な情報の定量的尺度はエントロピーと伝達情報量である エントロピーは確率変数の情報の尺度でありメッセージの圧縮しやすさの度合いである 伝達情報量は2つの確率変数間に共通する情報の尺度であり通信路における. R R によって描写されているとき X の期待値は E X x X Ω x f x と定義されます. 相互情報量は相互というだけあって2つの事象に関わる概念ですここで全く別系列だが互いに関連している2つの事象をa bとした時例えばa風邪か風邪でないかb熱があるかないかエントロピー hahb はそれぞれaという事象が持つ曖昧さとbという事象が持つ曖昧さ.
であるとき確率変数𝑋𝑋のエントロピーを 𝐻𝐻𝑋𝑋 𝑖𝑖1 𝑀𝑀 𝑝𝑝 𝑖𝑖 log 2 𝑝𝑝 𝑖𝑖 ビットと定義する 8 定義. X の値域 X Ω が可算集合である場合 X の期待値は無限級数になりますが. こんにちはももやまです 今回は情報理論で習う情報量について簡単にまとめてみたいと思います 情報量エントロピーの理解には確率に関する知識が必須です 確率についてあ.
その上でそれぞれの実数 x R に対して確率変数 X が値 x をとる確率 f x P X x P ω Ω X ω x を値として定める関数 f. Ω R の確率分布が確率関数 f. R R を定義しこれを X の 確率関数 probability functionや 確率質量関数 probability mass functionなどと呼びます.
第2章確率統計 統計学の概念数学がその言語である 集合論の復習 確率には大きく2つある頻度確率客観確率とベイズ確率主観確率 確率の定義事象eventの導入 条件付き確率の導入 独立な事象の同時確率.

情報理論まとめ Qiita
第7章 確率入門 Jamoviで学ぶ心理統計

2018 163622号 製造不良原因の探索支援方法及び情報処理装置 Astamuse

確率 統計 第12回 統計学の基礎1 ここです 確率論とは 確率変数 確率分布 確率変数の独立性 確率変数の平均 Ppt Download

確率 統計 第12回 統計学の基礎1 ここです 確率論とは 確率変数 確率分布 確率変数の独立性 確率変数の平均 Ppt Download
2
2

My Notebook 情報工学 情報理論 Note Md At Master Yagami360 My Notebook Github
You have just read the article entitled 情報理論 関連 2つの確率変数 その程度の関連. You can also bookmark this page with the URL : https://oreot3lu.blogspot.com/2022/07/2_0921273327.html
0 Response to "情報理論 関連 2つの確率変数 その程度の関連"
Post a Comment